常见的量子门
量子线路上常见的量子门
Pauli-X 门
X 门也称为泡利-X 门(Pauli-X gate), 它作用在单量子比特上, 与经典计算机上的NOT门等价, 将量子态进行翻转, 量子态变化方式如下:
Pauli-X门矩阵形式为泡利矩阵$\sigma_x$, 即:
量子线路显示如下图:
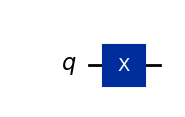
假设 NOT 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上, 可得到新的量子态如下:
Pauli-Y 门
Y 门也称为泡利-Y 门(Pauli-Y gate), 它作用在单量子比特上, 它的作用是能够使Bloch球上的箭头绕$Y$轴旋转角度$\pi$ .
Pauli-X门矩阵形式为泡利矩阵$\sigma_y$, 即:
量子线路显示如下图:

假设 NOT 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上, 可得到新的量子态如下:
Pauli-Z 门
Z 门也称为泡利-Z 门(Pauli-Z gate), 它作用在单量子比特上, 它的作用是能够使Bloch球上的箭头绕$Z$轴旋转角度$\pi$ .
Pauli-X门矩阵形式为泡利矩阵$\sigma_z$, 即:
量子线路显示如下图:

假设 NOT 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上, 可得到新的量子态如下:
Hadamard (H)门
Hadamard 门是一种可将基态变为叠加态的量子逻辑门, 简称为H门, 它作用在单比特上, 它对量子基态的变化方式如下:
Hadamard 门矩阵形式为:
量子线路显示如下图:
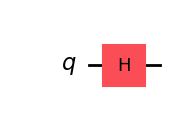
假设 Hadamard 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上, 可得到新的量子态如下:
S 门
S 门,也称为相位门,是一种单量子比特量子逻辑门,它主要改变量子态的相位,而不改变状态的概率幅。S 门的作用效果如下:
S 门的矩阵形式为:
量子线路显示如下图:
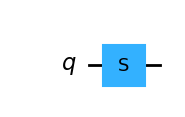
假设 S 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上,可得到新的量子态如下:
从上面的表达式可以看出,S 门将量子态 $|1\rangle$ 的相位旋转了 $90^\circ$ 或 $\pi/2$ 弧度,而量子态 $|0\rangle$ 的相位保持不变。
T 门
T 门,也称为π/8门,是一种单量子比特量子逻辑门,它在量子计算中用于实现较小的相位旋转。T 门的作用是对量子态的|1⟩分量施加一个相位变换,而|0⟩分量保持不变。T 门的效果如下:
这里 $e^{i\pi/4}$ 是复平面单位圆上的一个点,表示相位旋转π/4。
T 门的矩阵形式为:
量子线路显示如下图::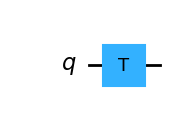
假设 T 门作用在任意量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 上,可得到新的量子态如下:
从上面的表达式可以看出,T 门将量子态 $|1\rangle$ 的相位旋转了 $45^\circ$ 或 $\pi/4$ 弧度,而量子态 $|0\rangle$ 的相位保持不变。
CNOT(Control-NOT) 门
CNOT 门,也称为控制非门,是一种双量子比特量子逻辑门,它在量子计算中用于实现量子比特之间的纠缠。CNOT 门有一个控制量子比特和一个目标量子比特。当控制量子比特为 |1⟩ 状态时,它将翻转目标量子比特的状态;如果控制量子比特为 |0⟩,则目标量子比特的状态保持不变。CNOT 门的作用效果如下:
CNOT 门的矩阵形式为:
量子线路显示如下图: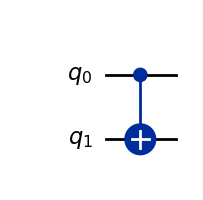
假设 CNOT 门作用在两个量子比特的任意态 $|\psi\rangle=\alpha|00\rangle+\beta|01\rangle+\gamma|10\rangle+\delta|11\rangle$ 上,可得到新的量子态如下:
从上面的表达式可以看出,CNOT 门会根据控制量子比特的状态来翻转目标量子比特的状态。
SWAP 门
SWAP 门是一种双量子比特量子逻辑门,它在量子计算中用于交换两个量子比特的状态。SWAP 门的作用效果如下:
SWAP 门的矩阵形式为:
量子线路显示如下图:
假设 SWAP 门作用在两个量子比特的任意态 $|\psi\rangle=\alpha|00\rangle+\beta|01\rangle+\gamma|10\rangle+\delta|11\rangle$ 上,可得到新的量子态如下:
从上面的表达式可以看出,SWAP 门会交换量子态 |01⟩ 和 |10⟩ 的状态,而量子态 |00⟩ 和 |11⟩ 保持不变。
iSWAP 门
iSWAP 门是另一种双量子比特量子逻辑门,它是 SWAP 门的一种变体。iSWAP 门不仅交换两个量子比特的状态,还引入了一个相对相位。iSWAP 门的作用效果如下:
iSWAP 门的矩阵形式为:
量子线路显示如下图: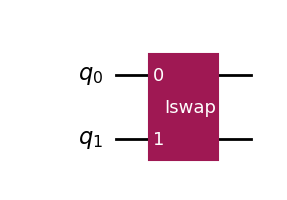
假设 iSWAP 门作用在两个量子比特的任意态 $|\psi\rangle=\alpha|00\rangle+\beta|01\rangle+\gamma|10\rangle+\delta|11\rangle$ 上,可得到新的量子态如下:
从上面的表达式可以看出,iSWAP 门会交换量子态 |01⟩ 和 |10⟩ 的状态,并在交换过程中引入一个相对相位, 量子态 |00⟩ 和 |11⟩ 保持不变。
Control-Z 门(CZ门)
Control-Z 门,也称为CZ门,是量子计算中的一种双量子比特量子逻辑门。CZ门的作用效果如下:
CZ门的矩阵形式为:
量子线路图如下所示: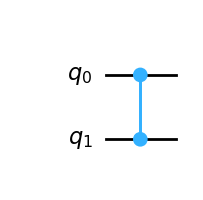
假设有两个量子比特初始状态为 $|\psi\rangle=\alpha|00\rangle+\beta|01\rangle+\gamma|10\rangle+\delta|11\rangle$,当CZ门作用在这个态上时,新的量子态 $|\psi’\rangle$ 将会变为:
从上面的表达式可以看出,只有当两个量子比特都处于|1⟩态时,CZ门才会对量子态产生相位翻转。
Toffoli 门
Toffoli 门,也称为 CCNOT(CCX, TOFF) 门,是量子计算中的一种三量子比特量子逻辑门。Toffoli 门在量子电路中用于在两个控制比特都为 |1⟩ 态时,对目标比特执行 NOT 操作(即翻转其状态)。Toffoli 门的作用效果如下:
这里,前两个量子比特是控制比特,第三个量子比特是目标比特。只有当两个控制比特都为 |1⟩ 时,目标比特的状态才会发生翻转。
Toffoli 门的矩阵形式为:
具体的量子线路图如下所示:
假设有三个量子比特初始状态为 $|\psi\rangle=\alpha|000\rangle+\beta|001\rangle+\gamma|010\rangle+\delta|011\rangle+\epsilon|100\rangle+\zeta|101\rangle+\eta|110\rangle+\theta|111\rangle$,当Toffoli门作用在这个态上时,新的量子态 $|\psi’\rangle$ 将会变为:
从上面的表达式可以看出,只有当两个控制比特都处于 |1⟩ 态时,Toffoli门才会对目标比特的状态产生翻转。
测量操作
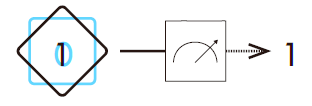
我们可以将测量视为一种量子门, 测量具有改变量子比特状态并确定其到底是0 还是1 的作用. 通过测量, 我们可以由量子比特所处的叠加态得到非0 即1 的经典比特的状态.
测量操作在线路上的显示如图:
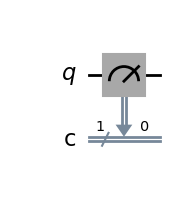
直到测量的那一瞬间, 量子态才变为确定的状态.